İçerik

• adımlar
• Yöntem 1/3: Bölüm 1: Bükülme Noktasını Belirleme
• Yöntem 2/3: Bir Fonksiyonun Türevlerini Hesaplama
• Yöntem 3/3: Bölüm 3: Bükülme Noktasını Bulun
• İpuçları

Diferansiyel hesapta, bir bükülme noktası, eğriliğinin işaret değiştirdiği (artıdan eksiye veya eksiden artıya) bir eğri üzerindeki bir noktadır. Bu kavram, verilerdeki önemli değişiklikleri belirlemek için makine mühendisliği, ekonomi ve istatistikte kullanılır.

adımlar

Yöntem 1/3: Bölüm 1: Bükülme Noktasını Belirleme

1. 1 Bir içbükey fonksiyonun tanımı. Bir içbükey fonksiyonun grafiğinin herhangi bir kirişinin (iki noktayı birleştiren bir parça) ortası, grafiğin altında veya üzerinde bulunur.
2. 2 Bir dışbükey fonksiyonun tanımı. Bir dışbükey fonksiyonun grafiğinin herhangi bir kirişinin (iki noktayı birleştiren bir parça) ortası, grafiğin üzerinde veya üzerinde bulunur.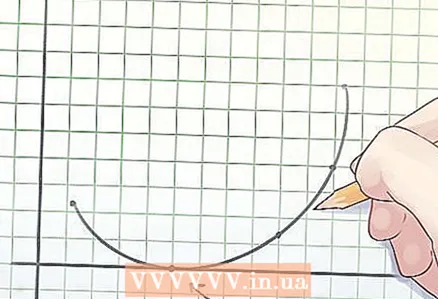
3. 3 Fonksiyonun köklerinin belirlenmesi. Bir fonksiyonun kökü, y = 0 olan "x" değişkeninin değeridir.
   • Bir fonksiyonu çizerken, kökler grafiğin x eksenini kestiği noktalardır.

Yöntem 2/3: Bir Fonksiyonun Türevlerini Hesaplama

1. 1 Fonksiyonun ilk türevini bulun. Ders kitabındaki farklılaşma kurallarına bakın; ilk türevleri nasıl alacağınızı öğrenmeniz ve ancak o zaman daha karmaşık hesaplamalara geçmeniz gerekir. Birinci türevler f '(x) olarak gösterilir. ax ^ p + bx ^ (p − 1) + cx + d biçimindeki ifadeler için, birinci türev: apx ^ (p − 1) + b (p - 1) x ^ (p − 2) + c'dir.
   • Örneğin, f (x) = x ^ 3 + 2x -1 fonksiyonunun bükülme noktalarını bulun. Bu fonksiyonun ilk türevi:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Fonksiyonun ikinci türevini bulun. İkinci türev, orijinal fonksiyonun birinci türevinin türevidir. İkinci türev f ′ ′ (x) olarak gösterilir.
   • Yukarıdaki örnekte, ikinci türev:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 İkinci türevi sıfıra ayarlayın ve elde edilen denklemi çözün. Sonuç, beklenen bükülme noktası olacaktır.
   • Yukarıdaki örnekte, hesaplamanız şöyle görünür:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Fonksiyonun üçüncü türevini bulun. Sonucunuzun aslında bir bükülme noktası olduğunu doğrulamak için, orijinal fonksiyonun ikinci türevinin türevi olan üçüncü türevi bulun. Üçüncü türev f ′ ′ ′ (x) olarak gösterilir.
   • Yukarıdaki örnekte, üçüncü türev:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Yöntem 3/3: Bölüm 3: Bükülme Noktasını Bulun

1. 1 Üçüncü türevi kontrol edin. Bir bükülme noktasını tahmin etmek için standart kural, eğer üçüncü türev sıfır değilse (yani, f ′ ′ ′ (x) ≠ 0), o zaman bükülme noktası gerçek bükülme noktasıdır. Üçüncü türevi kontrol edin; sıfır değilse, gerçek bükülme noktasını buldunuz.
   • Yukarıdaki örnekte üçüncü türev 0 değil 6'dır.Yani gerçek bükülme noktasını buldunuz.
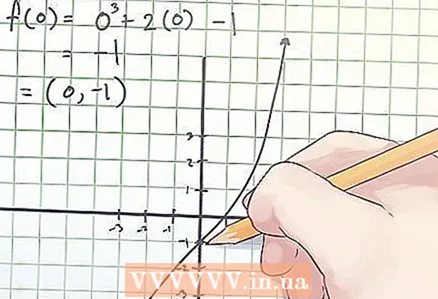2. 2 Büküm noktasının koordinatlarını bulun. Bükülme noktası koordinatları (x, f (x)) olarak gösterilir; burada x, "x" bağımsız değişkeninin bükülme noktasındaki değeridir, f (x) bükülme noktasındaki "y" bağımlı değişkeninin değeridir. nokta.
   • Yukarıdaki örnekte, ikinci türevi sıfıra eşitlerken x = 0 olduğunu buldunuz. Dolayısıyla, bükülme noktasının koordinatlarını belirlemek için f (0)'ı bulun. Hesaplamanız şöyle görünür:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = -1.
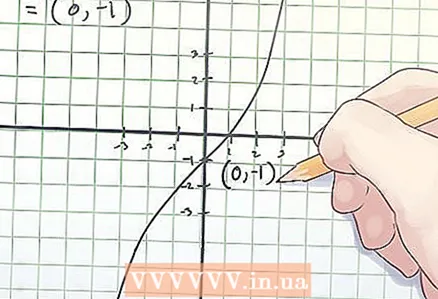3. 3 Bükülme noktasının koordinatlarını yazın. Bükülme noktası koordinatları bulunan x ve f(x) değerleridir.
   • Yukarıdaki örnekte, bükülme noktası (0, -1) koordinatlarındadır.

İpuçları

• Serbest terimin (asal sayı) ilk türevi her zaman sıfırdır.