İçerik

• adımlar
• Yöntem 1/3: Sabit terimsiz bir kübik denklem nasıl çözülür
• Yöntem 2/3: Çarpanları Kullanarak Tam Kökler Nasıl Bulunur
• Yöntem 3/3: Diskriminant Kullanarak Bir Denklem Nasıl Çözülür

Kübik bir denklemde en yüksek üs 3'tür, böyle bir denklemin 3 kökü (çözüm) vardır ve şu şekildedir: ${ displaystyle balta ^ {3} + bx ^ {2} + cx + d = 0}$... Bazı kübik denklemleri çözmek o kadar kolay değildir, ancak doğru yöntemi uygularsanız (iyi bir teorik altyapı ile), en karmaşık kübik denklemin bile köklerini bulabilirsiniz - bunun için ikinci dereceden denklemi çözmek için formülü kullanın, tüm kökleri veya diskriminantı hesaplayın.

adımlar

Yöntem 1/3: Sabit terimsiz bir kübik denklem nasıl çözülür

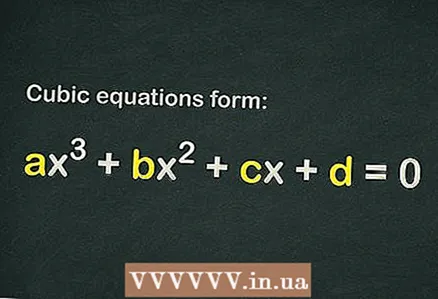1. 1 Kübik denklemde serbest terim olup olmadığını öğrenin NS{ görüntü stili d}. Kübik denklem forma sahiptir ${ displaystyle balta ^ {3} + bx ^ {2} + cx + d = 0}$... Bir denklemin kübik olarak kabul edilebilmesi için sadece terimin ${ görüntü stili x ^ {3}}$ (yani, başka hiçbir üye olmayabilir).
   • Denklemin serbest terimi varsa ${ görüntü stili d}$, farklı bir yöntem kullanın.
   • denklemde ise ${ görüntü stili a = 0}$, kübik değildir.
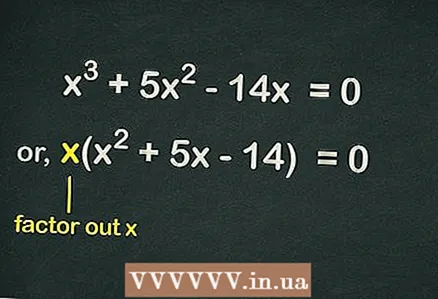2. 2 Parantezlerden çıkarın x{ görüntü stili x}. Denklemde serbest terim olmadığı için denklemdeki her terim değişkeni içerir. ${ görüntü stili x}$... Bu demektir ki bir ${ görüntü stili x}$ denklemi basitleştirmek için parantezlerin dışında tutulabilir. Böylece denklem şu şekilde yazılacaktır: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • Örneğin, bir kübik denklem verildi ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Çıkarmak ${ görüntü stili x}$ parantez ve olsun ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
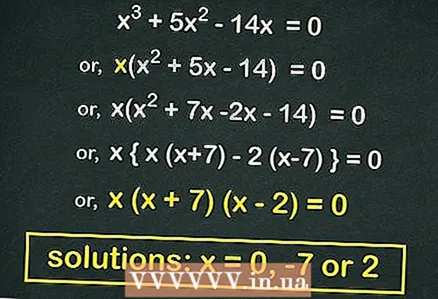3. 3 İkinci dereceden denklemi (mümkünse) çarpanı (iki iki terimlinin çarpımı). Formun birçok ikinci dereceden denklemi ${ displaystyle balta ^ {2} + bx + c = 0}$ faktörize edilebilir. çıkarırsak böyle bir denklem ortaya çıkar ${ görüntü stili x}$ parantez dışında. Örneğimizde:
   • Parantezlerden çıkarın ${ görüntü stili x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • İkinci dereceden denklemi çarpanlara ayırın: ${ görüntü stili x (x + 7) (x-2) = 0}$
   • Her kutuyu şuna eşitleyin: ${ görüntü stili 0}$... Bu denklemin kökleri ${ görüntü stili x = 0, x = -7, x = 2}$.
4. 4 Özel bir formül kullanarak ikinci dereceden bir denklemi çözün. İkinci dereceden denklem çarpanlara ayrılamıyorsa bunu yapın. Bir denklemin iki kökünü bulmak için katsayıların değerleri ${ görüntü stili a}$, ${ görüntü stili b}$, ${ görüntü stili c}$ formülde ikame ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • Örneğimizde, katsayıların değerlerini değiştirin ${ görüntü stili a}$, ${ görüntü stili b}$, ${ görüntü stili c}$ (${ görüntü stili 3}$, ${ görüntü stili -2}$, ${ görüntü stili 14}$) formüle:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ görüntü stili { frac {2 pm { sqrt {(4-168}}} {6}}})$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • İlk kök:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ görüntü stili { frac {2 + 12.8i} {6}}}$

   • İkinci kök:

     ${ görüntü stili { frac {2-12,8i} {6}}}$

5. 5 Kübik denklemin çözümleri olarak sıfır ve ikinci dereceden kökleri kullanın. İkinci dereceden denklemlerin iki kökü vardır, kübik denklemlerin ise üç kökü vardır. Zaten iki çözüm buldunuz - bunlar ikinci dereceden denklemin kökleridir. Parantezlerin dışına "x" koyarsanız, üçüncü çözüm şöyle olur: ${ görüntü stili 0}$.
   • Parantezlerden "x" çıkarırsanız, ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, yani iki faktör: ${ görüntü stili x}$ ve parantez içinde ikinci dereceden bir denklem. Bu faktörlerden herhangi biri ise ${ görüntü stili 0}$, tüm denklem de eşittir ${ görüntü stili 0}$.
   • Böylece, ikinci dereceden bir denklemin iki kökü bir kübik denklemin çözümleridir. Üçüncü çözüm ise ${ görüntü stili x = 0}$.

Yöntem 2/3: Çarpanları Kullanarak Tam Kökler Nasıl Bulunur

1. 1 Kübik denklemde serbest bir terim olduğundan emin olun NS{ görüntü stili d}. Formun bir denkleminde ise ${ displaystyle balta ^ {3} + bx ^ {2} + cx + d = 0}$ ücretsiz üye var ${ görüntü stili d}$ (sıfıra eşit değildir), parantezlerin dışına "x" koymak işe yaramaz. Bu durumda, bu bölümde özetlenen yöntemi kullanın.
   • Örneğin, verilen bir kübik denklem ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Denklemin sağ tarafında sıfır almak için ekleyin ${ görüntü stili 6}$ denklemin her iki tarafına
   • denklem ortaya çıkacak ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Olarak ${ görüntü stili d = 6}$, ilk bölümde açıklanan yöntem kullanılamaz.
2. 2 Katsayının faktörlerini yazın a{ görüntü stili a} ve ücretsiz üye NS{ görüntü stili d}. Yani, sayının çarpanlarını bulun ${ görüntü stili x ^ {3}}$ ve eşittir işaretinden önceki sayılar. Bir sayının çarpanlarının çarpıldığında o sayıyı veren sayılar olduğunu hatırlayın.
   • Örneğin, numarayı almak için 6, çarpmanız gerekiyor ${ displaystyle 6 kere 1}$ ve ${ displaystyle 2 kere 3}$... yani sayılar 1, 2, 3, 6 sayının çarpanlarıdır 6.
   • denklemimizde ${ görüntü stili a = 2}$ ve ${ görüntü stili d = 6}$... çarpanlar 2 NS 1 ve 2... çarpanlar 6 sayılar mı 1, 2, 3 ve 6.
3. 3 Her faktörü böl a{ görüntü stili a} her faktör için NS{ görüntü stili d}. Sonuç olarak, çok sayıda kesir ve birkaç tam sayı elde edersiniz; kübik denklemin kökleri tamsayılardan biri veya tamsayılardan birinin negatif değeri olacaktır.
   • Örneğimizde, faktörleri bölün ${ görüntü stili a}$ (1 ve 2) faktörlere göre ${ görüntü stili d}$ (1, 2, 3 ve 6). Alacaksınız: ${ görüntü stili 1}$, ${ görüntü stili { frac {1} {2}}}$, ${ görüntü stili { frac {1} {3}}}$, ${ görüntü stili { frac {1} {6}}}$, ${ görüntü stili 2}$ ve ${ görüntü stili { frac {2} {3}}}$... Şimdi elde edilen kesirlerin ve sayıların negatif değerlerini bu listeye ekleyin: ${ görüntü stili 1}$, ${ görüntü stili -1}$, ${ görüntü stili { frac {1} {2}}}$, ${ görüntü stili - { frac {1} {2}}}$, ${ görüntü stili { frac {1} {3}}}$, ${ görüntü stili - { frac {1} {3}}}$, ${ görüntü stili { frac {1} {6}}}$, ${ görüntü stili - { frac {1} {6}}}$, ${ görüntü stili 2}$, ${ görüntü stili -2}$, ${ görüntü stili { frac {2} {3}}}$ ve ${ görüntü stili - { frac {2} {3}}}$... Kübik denklemin tüm kökleri bu listedeki bazı sayılardır.
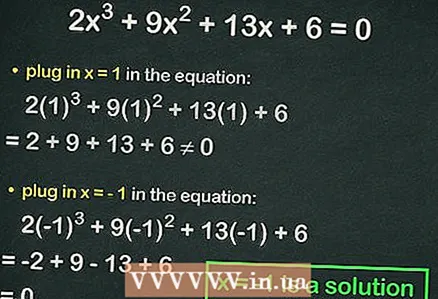4. 4 Kübik denkleme tam sayıları girin. Eşitlik doğruysa, ikame edilen sayı denklemin köküdür. Örneğin, denklemde yerine ${ görüntü stili 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, yani eşitlik gözlenmez. Bu durumda, bir sonraki numarayı takın.
   • Vekil ${ görüntü stili -1}$: ${ görüntü stili (-2) +9 + (- 13) +6}$ = 0. Böylece, ${ görüntü stili -1}$ denklemin tüm köküdür.
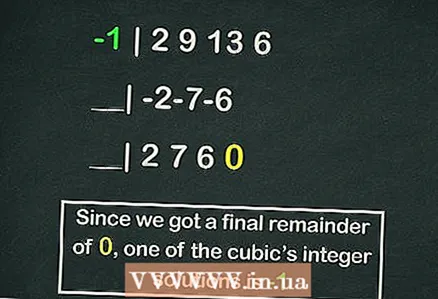5. 5 Polinomları bölme yöntemini kullanın Horner'ın planıdenklemin köklerini daha hızlı bulmak için Sayıları denklemde manuel olarak değiştirmek istemiyorsanız bunu yapın. Horner'ın şemasında, tamsayılar denklemin katsayılarının değerlerine bölünür. ${ görüntü stili a}$, ${ görüntü stili b}$, ${ görüntü stili c}$ ve ${ görüntü stili d}$... Sayılar eşit olarak bölünebiliyorsa (yani kalan ${ görüntü stili 0}$), bir tamsayı denklemin köküdür.
   • Horner'ın şeması ayrı bir makaleyi hak ediyor, ancak aşağıdaki, bu şemayı kullanarak kübik denklemimizin köklerinden birinin hesaplanmasına bir örnek:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Yani kalan ${ görüntü stili 0}$, ancak ${ görüntü stili -1}$ denklemin köklerinden biridir.

Yöntem 3/3: Diskriminant Kullanarak Bir Denklem Nasıl Çözülür

1. 1 Denklemin katsayılarının değerlerini yazın a{ görüntü stili a}, B{ görüntü stili b}, C{ görüntü stili c} ve NS{ görüntü stili d}. İleride kafanızın karışmaması için belirtilen katsayıların değerlerini önceden yazmanızı tavsiye ederiz.
   • Örneğin, verilen denklem ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$... bir yere yaz ${ görüntü stili a = 1}$, ${ görüntü stili b = -3}$, ${ görüntü stili c = 3}$ ve ${ görüntü stili d = -1}$... Hatırlayın, eğer daha önce ${ görüntü stili x}$ sayı yok, karşılık gelen katsayı hala var ve eşittir ${ görüntü stili 1}$.
2. 2 Özel bir formül kullanarak sıfır diskriminantı hesaplayın. Diskriminant kullanarak kübik bir denklemi çözmek için bir takım zor hesaplamalar yapmanız gerekir, ancak tüm adımları doğru bir şekilde gerçekleştirirseniz, bu yöntem en karmaşık kübik denklemleri çözmek için vazgeçilmez hale gelecektir. İlk hesaplama ${ görüntü stili Delta _ {0}}$ (sıfır diskriminant) ihtiyacımız olan ilk değerdir; bunu yapmak için formüldeki karşılık gelen değerleri değiştirin ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Diskriminant, bir polinomun köklerini karakterize eden bir sayıdır (örneğin, ikinci dereceden bir denklemin diskriminantı aşağıdaki formülle hesaplanır). ${ displaystyle b ^ {2} -4ac}$).
   • Bizim denklemimizde:

     ${ displaystyle b ^ {2} -3ac}$

     ${ görüntü stili (-3) ^ {2} -3 (1) (3)}$

     ${ görüntü stili 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Formülü kullanarak ilk diskriminantı hesaplayın Δ1=2B3−9aBC+27a2NS{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. İlk ayrımcı ${ görüntü stili Delta _ {1}}$ - bu ikinci önemli değerdir; hesaplamak için karşılık gelen değerleri belirtilen formüle takın.
   • Bizim denklemimizde:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ görüntü stili -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Hesaplamak:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Yani, elde edilen değerler aracılığıyla kübik denklemin diskriminantını bulun. ${ görüntü stili Delta _ {0}}$ ve ${ görüntü stili Delta _ {1}}$... Bir kübik denklemin diskriminantı pozitifse denklemin üç kökü vardır; diskriminant sıfır ise denklemin bir veya iki kökü vardır; diskriminant negatif ise denklemin bir kökü vardır.
   • Kübik bir denklemin her zaman en az bir kökü vardır, çünkü bu denklemin grafiği X eksenini en az bir noktada keser.
   • denklemimizde ${ görüntü stili Delta _ {0}}$ ve ${ görüntü stili Delta _ {1}}$ eşittir ${ görüntü stili 0}$, böylece kolayca hesaplayabilirsiniz ${ görüntü stili Delta}$:

     ${ görüntü stili ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ görüntü stili ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ görüntü stili 0 = Delta}$... Dolayısıyla denklemimizin bir veya iki kökü vardır.

5. 5 Hesaplamak:${ displaystyle C = ^ {3} { sqrt { sol ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1) } sağ) div 2}}}$. ${ görüntü stili C}$ - bu bulunan son önemli miktardır; denklemin köklerini hesaplamanıza yardımcı olacaktır. Değerleri belirtilen formülde değiştirin ${ görüntü stili Delta _ {1}}$ ve ${ görüntü stili Delta _ {0}}$.
   • Bizim denklemimizde:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ görüntü stili 0 = C}$

6. 6 Denklemin üç kökünü bulun. Formül ile yapın ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, nerede ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, ancak n eşittir 1, 2 veya 3... Bu formülde uygun değerleri değiştirin - sonuç olarak denklemin üç kökünü alacaksınız.
   • Aşağıdaki formülü kullanarak değeri hesaplayın n = 1, 2 veya 3ve ardından cevabı kontrol edin. Cevabınızı kontrol ettiğinizde 0 alırsanız, bu değer denklemin köküdür.
   • Örneğimizde, yerine 1 içinde ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$ ve Al 0, yani 1 denklemin köklerinden biridir.